
点击照片看详细介绍
刘辉 中国古代数学家, 曾给九章算术作注,计算圆周率 π,精确到了小数点后第四位。

点击照片看详细介绍
祖冲之 中国古代数学家、天文学家,他计算圆周率 π,精确到了小数点后第七位, π 的近似值 355/113 也是他提出来的,称为密率。

点击照片看详细介绍
In 1824 Abel proved the impossibility of solving algebraically the general equation of the fifth degree.

点击照片看详细介绍
Archimedes was the greatest mathematician of his age. His contributions in geometry revolutionised the subject and his methods anticipated the integral calculus 2,000 years before Newton and Leibniz. He was also a thoroughly practical man who invented a wide variety of machines including pulleys and the Archimidean screw pumping device.

点击照片看详细介绍
Jacob Bernoulli was a Swiss mathematician who was the first to use the term integral. He studied the catenary, the curve of a suspended string. He was an early user of polar coordinates and discovered the isochrone.

点击照片看详细介绍
Bolzano successfully freed calculus from the concept of the infinitesimal. He also gave examples of 1-1 correspondences between the elements of an infinite set and the elements of a proper subset.

点击照片看详细介绍
Cantor founded set theory and introduced the concept of infinite numbers with his discovery of cardinal numbers. He also advanced the study of trigonometric series.

点击照片看详细介绍
Cauchy pioneered the study of analysis, both real and complex, and the theory of permutation groups. He also researched in convergence and divergence of infinite series, differential equations, determinants, probability and mathematical physics.

点击照片看详细介绍
Jean d'Alembert was a a French mathematician who was a pioneer in the study of differential equations and their use of in physics. He studied the equilibrium and motion of fluids.

点击照片看详细介绍
Darboux made important contributions to differential geometry and analysis and the Darboux integral is named after him.

点击照片看详细介绍
Dedekind's major contribution was a redefinition of irrational numbers in terms of Dedekind cuts. He introduced the notion of an ideal which is fundamental to ring theory.

点击照片看详细介绍

点击照片看详细介绍
Dirichlet proved in 1826 that in any arithmetic progression with first term coprime to the difference there are infinitely many primes.

点击照片看详细介绍
Leonhard Euler was a Swiss mathematician who made enormous contibutions to a wide range of mathematics and physics including analytic geometry, trigonometry, geometry, calculus and number theory.

点击照片看详细介绍
Pierre de Fermat was a French lawyer and government official most remembered for his work in number theory; in particular for Fermat's Last Theorem. He is also important in the foundations of the calculus.

点击照片看详细介绍
Fourier studied the mathematical theory of heat conduction. He established the partial differential equation governing heat diffusion and solved it by using infinite series of trigonometric functions.

点击照片看详细介绍
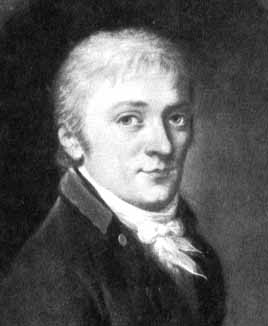
点击照片看详细介绍
Gauss worked in a wide variety of fields in both mathematics and physics incuding number theory, analysis, differential geometry, geodesy, magnetism, astronomy and optics. His work has had an immense influence in many areas.

点击照片看详细介绍
Jacques Hadamard was a French mathematician whose most important result is the prime number theorem which he proved in 1896. This states that the number of primes < n tends to infinity as fast as n/log e n.

点击照片看详细介绍
Hölder worked on the convergence of Fourier series and in 1884 he discovered the inequality now named after him. He became interested in group theory through Kronecker and Klein and proved the uniqueness of the factor groups in a composition series.

点击照片看详细介绍
Kummer's main achievement was the extension of results about the integers to other integral domains by introducing the concept of an ideal.

点击照片看详细介绍
Lagrange excelled in all fields of analysis and number theory and analytical and celestial mechanics.

点击照片看详细介绍
Lebesgue formulated the theory of measure in 1901 and the following year he gave the definition of the Lebesgue integral that generalises the notion of the Riemann integral.

点击照片看详细介绍
Gottfried Leibniz was a German mathematician who developed the present day notation for the differential and integral calculus though he never thought of the derivative as a limit. His philosophy is also important and he invented an early calculating machine.

点击照片看详细介绍
De L'Hôpital was a French mathematician who wrote the first textbook on calculus, which consisted of the lectures of his teacher Johann Bernoulli.

点击照片看详细介绍
Lipschitz is remembered for the "Lipschitz condition", an inequality that guarantees a unique solution to the differential equation y' = f (x, y).

点击照片看详细介绍
Colin Maclaurin was a Scottish mathematican who published the first systematic exposition of Newton's methods, written as a reply to Berkeley's attack on the calculus for its lack of rigorous foundations.

点击照片看详细介绍

点击照片看详细介绍
Peano was the founder of symbolic logic and his interests centred on the foundations of mathematics and on the development of a formal logical language.

点击照片看详细介绍
Paul du Bois-Reymond gave a continuous function whose Fourier series diverges at every point.

点击照片看详细介绍
Riemann's ideas concerning geometry of space had a profound effect on the development of modern theoretical physics. He clarified the notion of integral by defining what we now call the Riemann integral.

点击照片看详细介绍
Stokes established the science of hydrodynamics with his law of viscosity describing the velocity of a small sphere through a viscous fluid.

点击照片看详细介绍

点击照片看详细介绍
Brook Taylor was an English mathematician who added to mathematics a new branch now called the 'calculus of finite differences', invented integration by parts, and discovered the celebrated formula known as Taylor's expansion.

点击照片看详细介绍
John Wallis was an English mathematician who built on Cavalieri's method of indivisibles to devise a method of interpolation. Using Kepler's concept of continuity he discovered methods to evaluate integrals.

点击照片看详细介绍
Weierstrass is best known for his construction of the theory of complex functions by means of power series.