
量子计算机运算与量子纠缠论文介绍

- 论文题目
- 英文摘要
We derive a general spherical coordinate formula for a quantum state of n-qubit register and study n-qubit operation rules on (n+1)
-sphere with the target to help developing a (photon or other technique)-based programmable quantum computer. The newly developed
angle-based n-qubit operation rules are simple and efficient, which reduce the complicated quantum multiplication and division
operations to simple addition and subtraction operations just like those used in a conventional computer. The rules for n-qubit
operations are realized through measurement-based feedback controls and quantum entanglements. In the meanwhile, we derive the
scaling limits (called reflecting Gaussian random fields on a (n+1)-sphere) for n-qubit quantum computer-based queueing systems
under two different heavy traffic regimes. The queueing systems are with multiple classes of users and batch quantum random walks
over the (n+1)-sphere as arrival inputs. In the first regime, the qubit number n is fixed and the scaling is in terms of both time
and space. Under this regime, performance modeling during deriving the scaling limit in terms of balancing the arrival and service
rates under first-in first-out and work-conserving service policy is conducted. In the second regime, besides the time and space
scaling parameters, the qubit number n itself is also considered as a varying scaling parameter with the additional aim to find a
suitable number of qubits for the design of a quantum computer. This regime is in contrast to the well-known Halfin–Whitt regime.
- 中文介绍
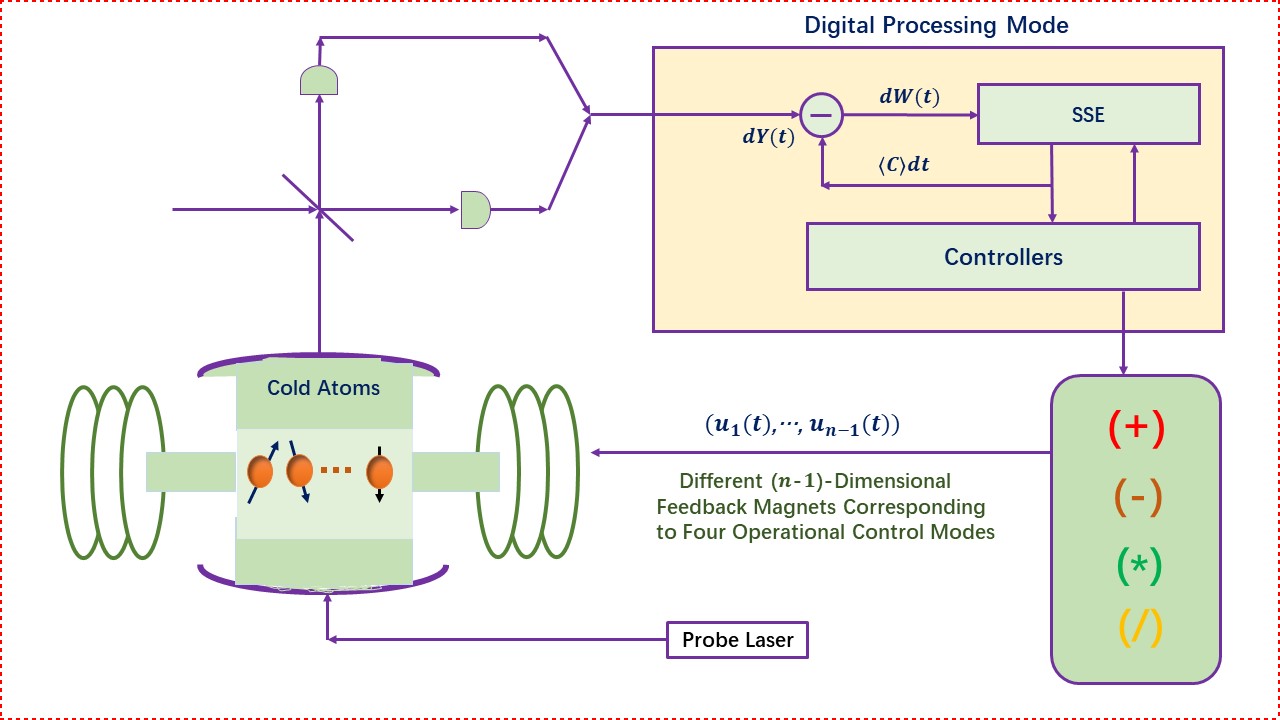
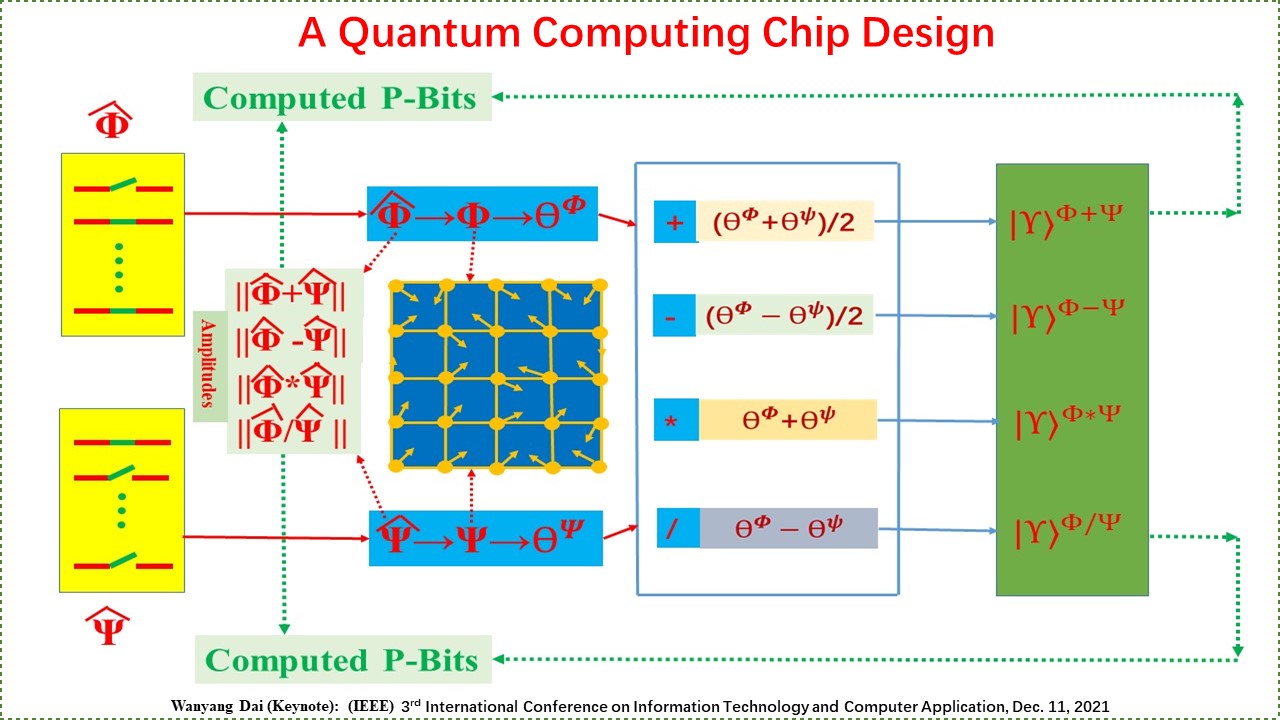
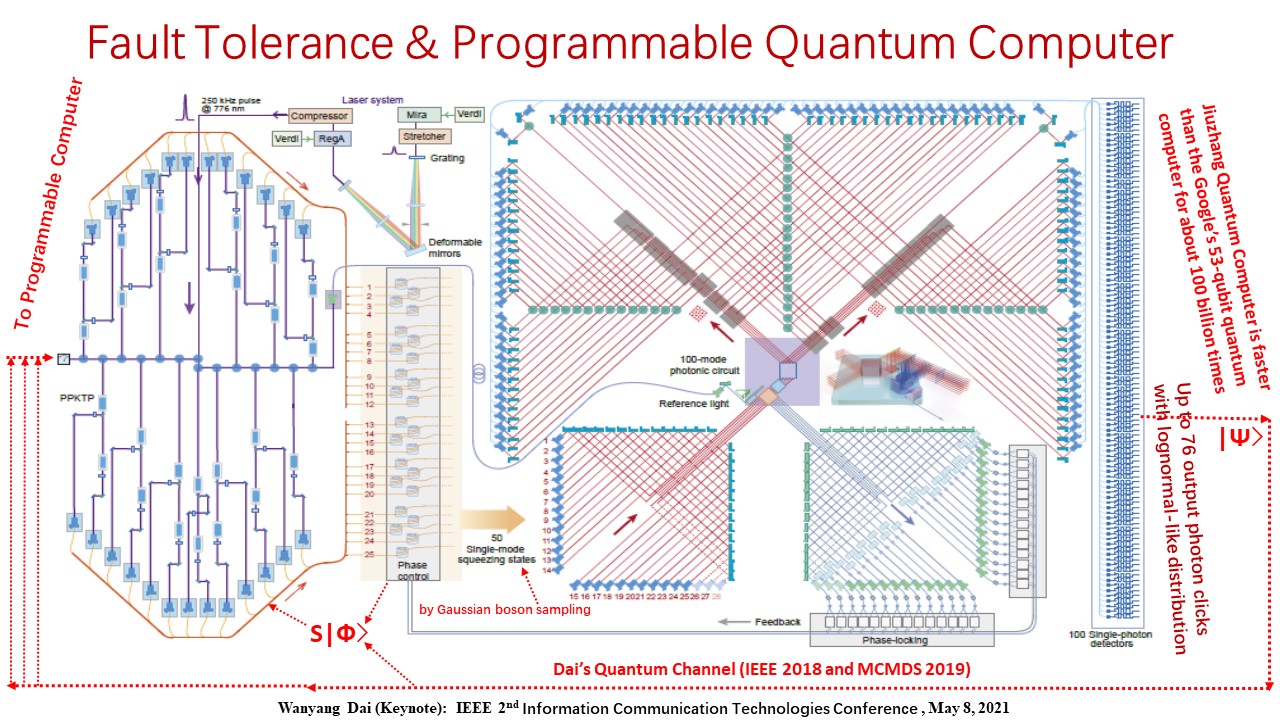
2018年我们在国际上发表了广义量子信道,可用于量子测量与通信等目的,一年半后,著名的“九章”量子计算机发表,其构架也可用我们的量子
信道来刻画,但这些成果都可归纳为“有芯无脑”,还不是可编程的。鉴于此,我们设计了有关量子计算机的运算法则,可将“乘”与“除”的运算转
化为“加”与“减”的运算,这便于传统计算机相对应了,而这种运算可通过量子纠缠芯片体系实现。另外,计算机运算与存储处理的性能也是计算
机领域的核心问题,因而针对不同量子位的构架,我们导出了相应的有限维黎曼流形(比如,球面)与无穷维黎曼流形(比如:无穷维球面)上
的反射高斯场作为有关量子计算机的性能评估模型。
- 关键词与关键技术
- Reflecting Gaussian random field on (n+1)-sphere, n-qubit quantum computer, quantum entanglement, queueing system, quantum
random walk, heavy traffic, Halfin-Whitt regime.
- 相关论文
- 点击这里查看更多相关论文


|