
机器学习金融大模型与倒向随机偏微分方程论文介绍

- 论文题目
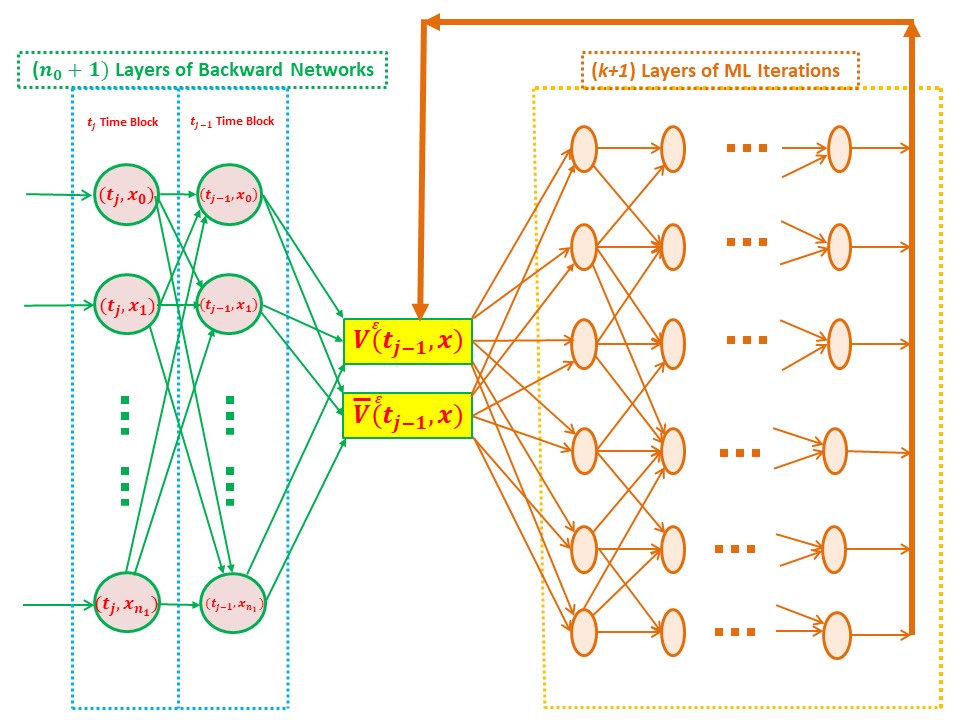
- 英文摘要
We have studied a strongly nonlinear backward stochastic partial differential equation (B-SPDE) through an approximation method
and with machine learning (ML)-based Monte Carlo simulation. This equation is well-known and was previously derived from studies
in finance. However, how to analyze and solve this equation has remained a problem for quite a long time. The main difficulty is
due to the singularity of the B-SPDE since it is a strongly nonlinear one. Therefore, by introducing new truncation operators
and integrating the machine learning technique into the platform of a convolutional neural network (CNN), we have developed an
effective approximation method with a Monte Carlo simulation algorithm to tackle the well-known open problem. In doing so, the
existence and uniqueness of a 2-tuple adapted strong solution to an approximation B-SPDE were proved. Meanwhile, the convergence
of a newly designed simulation algorithm was established. Simulation examples and an application in finance were also provided.
- 中文介绍
- 关键词与关键技术
- backward stochastic partial differential equation (B-SPDE); Monte Carlo simulation; strongly nonlinear; Cauchy terminal
value problem; machine learning (ML); convolutional neural network (CNN); Conditional expectation projection and big model regression.
- 相关论文
- 点击这里查看更多相关论文


|