随机优化与大数据空间点过程粒子晶格量子闪烁强度Stein估计论文介绍
- 论文题目及论文下载
- 英文摘要
We develop a global Stein estimator through Malliavin derivatives to estimate the multi-variable intensity functions of general d-dimensional
spatial inhomogeneous Poisson point processes (IPPPs). The gain performance between our Stein estimator and a tested maximum likelihood (ML)
estimator is analyzed via Malliavin calculus. In comparison with existing homogeneous studies, our inhomogeneous cases are more complex in a
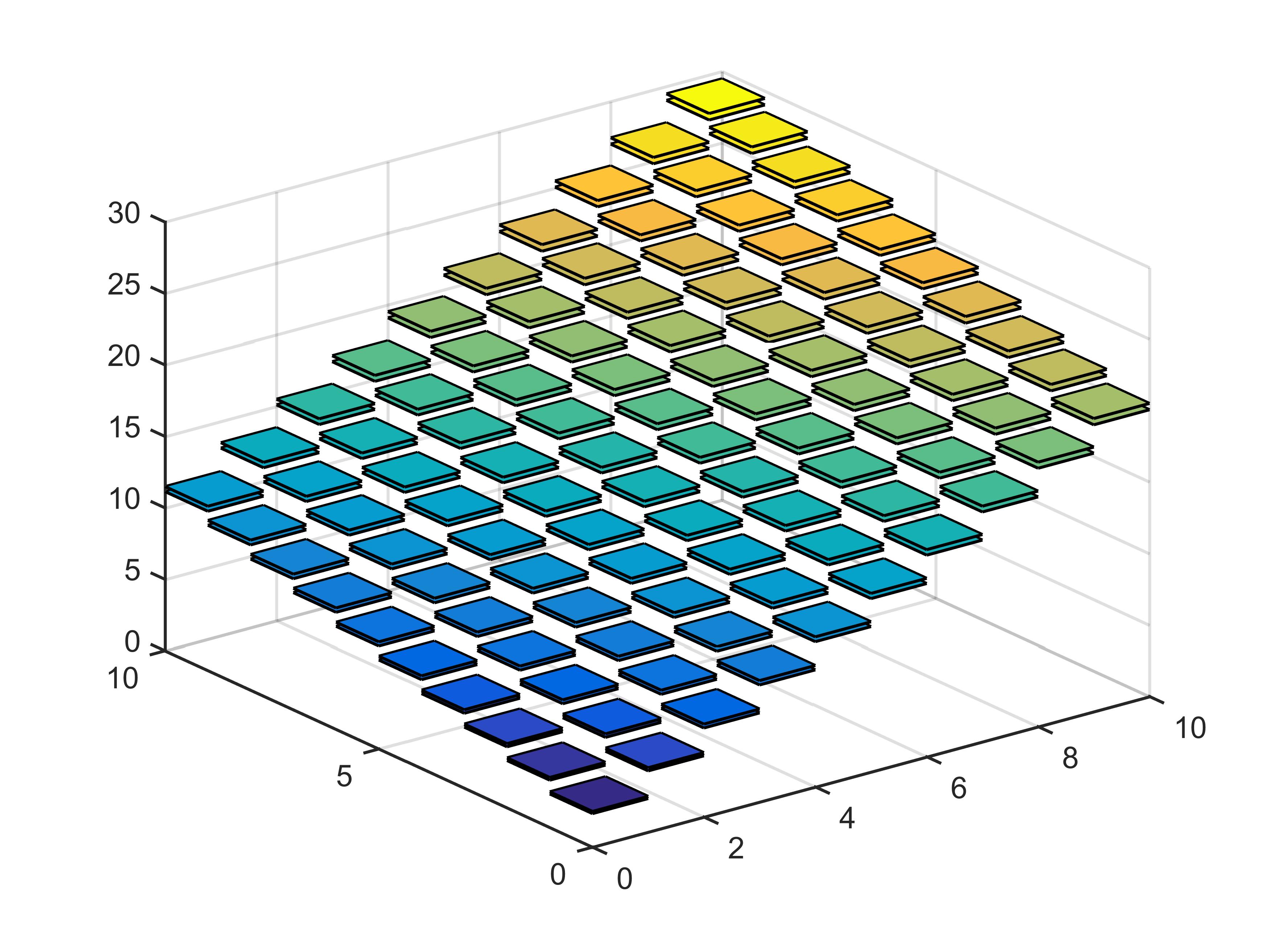
global way and more real in practice. In the numerical simulation experiments, our estimated intensity functions via the Stein estimator well
match the true one, which outperform the ones obtained by the ML estimator with an average gain larger than 30% concerning mean squared errors
(MSEs). Hence, our Stein method is more robust with smaller MSEs. We also establish the mean-squared convergence with error estimation for our
Stein estimator. Comparing with the existing study, our observation window for an IPPP is a d-dimensional rectangle and its boundary is not
C^{2}-smooth. This non-smoothness introduces additional complexity to our convergence analysis. Thus, a weak convergence approach is employed
to overcome this difficulty.
- 中文摘要
我们通过Malliavin导数发展出一种全局Stein估计器来估计一般d维空间中非齐次Poisson点过程的多变量强度函数。通过Malliavin积分，我们分析了所发展
的Stein估计器与用于测试的极大似然估计器之间的增益性能。与现存齐次的研究成果相比，我们非齐次的情况是全局更复杂的情况同时也更为实际。数值实
验表明，基与我们发展的Stein估计器所得的估计强度函数与其相应的真实强度函数相吻合，并且在均方误差的意义下，其平均估计增益要比极大似然估计器
要高出30%以上。因此，我们所发展的Stein估计器更加稳健且具有较小误差。另外，相比于现存研究，我们针对非齐次Poisson点过程所使用的观察窗口是一
个d维矩形体，因而，其边界不是二阶光滑的。这种非光滑性给我们的收敛性分析带来了附加的复杂性，因而，我们发展了一种弱收敛方法克服了这种困难。
- 关键词与关键技术
- Multi-variable intensity function, spatial inhomogeneous Poisson point process, Stein estimator, Malliavin calculus, big data
- 随机优化近年来受到很大关注，2018年世界数学家大会（ICM 2018）曾邀请了1小时报告，相比于确定性优化方法有诸多优点，关键在二阶导数随机扰动
的优化处理上。与这些经典随机优化的不同之处在于，我们考虑的是空间随机点过程泛函参变量函数的优化估计问题，因而我们的导数也不是经典的微分导数，
而是著名的Malliavin泛函导数，故而，我们随机优化参变量函数估计的关键是在二阶Malliavin泛函导数的处理上。数据实验表明我们设计的该Stein估计方法
比经典著名的优化方法极大势然估计要优越，可应用到大数据空间点过程分形与有限元粒子晶格量子闪烁强度估计及5G/6G与量子计算的有关问题上。另外，
基于Malliavin分析的Stein方法为什么比极大似然估计更优？正像反射扩散模型可对应于多种策略系统一样，可快可慢，可优可庸，但其极限点或其极限模型
可一样，故要选更快更优的路径，实际使用中才更有效，不过会更复杂与更困难。
- 相关论文
- W. Dai, Brownian approximations for queueing networks with finite buffers: modeling, heavy traffic analysis
and numerical implementations
 , Ph.D. Dissertation, Georgia Institute of
Technology, U.S.A., 1996, and UMI Dissertation Services (with Publishing No. 9714724), A Bell & Howell Company, 300 N. Zeeb Road, Ann Arbor,
Michigan 48106, U.S.A., 1997
- 点击这里查看更多相关论文
戴万阳享有诗词著作权与版权
|
